Install - pawari dictionary app  

Install - vidyarthi sanskrit dictionary app  

(1/f) = (1/v) + (1/u) दर्पण सूत्र की व्युत्पत्ति कीजिए | Derive The Mirror Formula

• BY:RF competition
• 11723
• 0
• Copy
• Share

दर्पण सूत्र– किसी गोलीय दर्पण की फोकस दूरी, ध्रुव से वस्तु की दूरी और प्रतिबिम्ब की दूरी के मध्य सम्बन्ध बताने वाले सूत्र को 'दर्पण सूत्र' कहा जाता है। दर्पण सूत्र, अवतल और उत्तल दर्पण दोनों के लिए एक समान होता है। दर्पण सूत्र को इस प्रकार व्यक्त किया जाता है–
(1⁄f) = (1⁄v) + (1⁄u)

Mirror Formula– The formula that gives the relation between the focal length of a spherical mirror, the distance of the object from the pole and the distance of the image is called 'mirror formula'. The mirror formula is the same for both concave and convex mirrors. The mirror formula is expressed as–
(1⁄f) = (1⁄v) + (1⁄u)

भौतिक विज्ञान के इन 👇 प्रकरणों को भी पढ़ें। (Also read these 👇 episodes of Physics.)
गोलीय दर्पण के लिए चिह्न परिपाटी एवं इसके नियम | Mark Convention And Its Rules

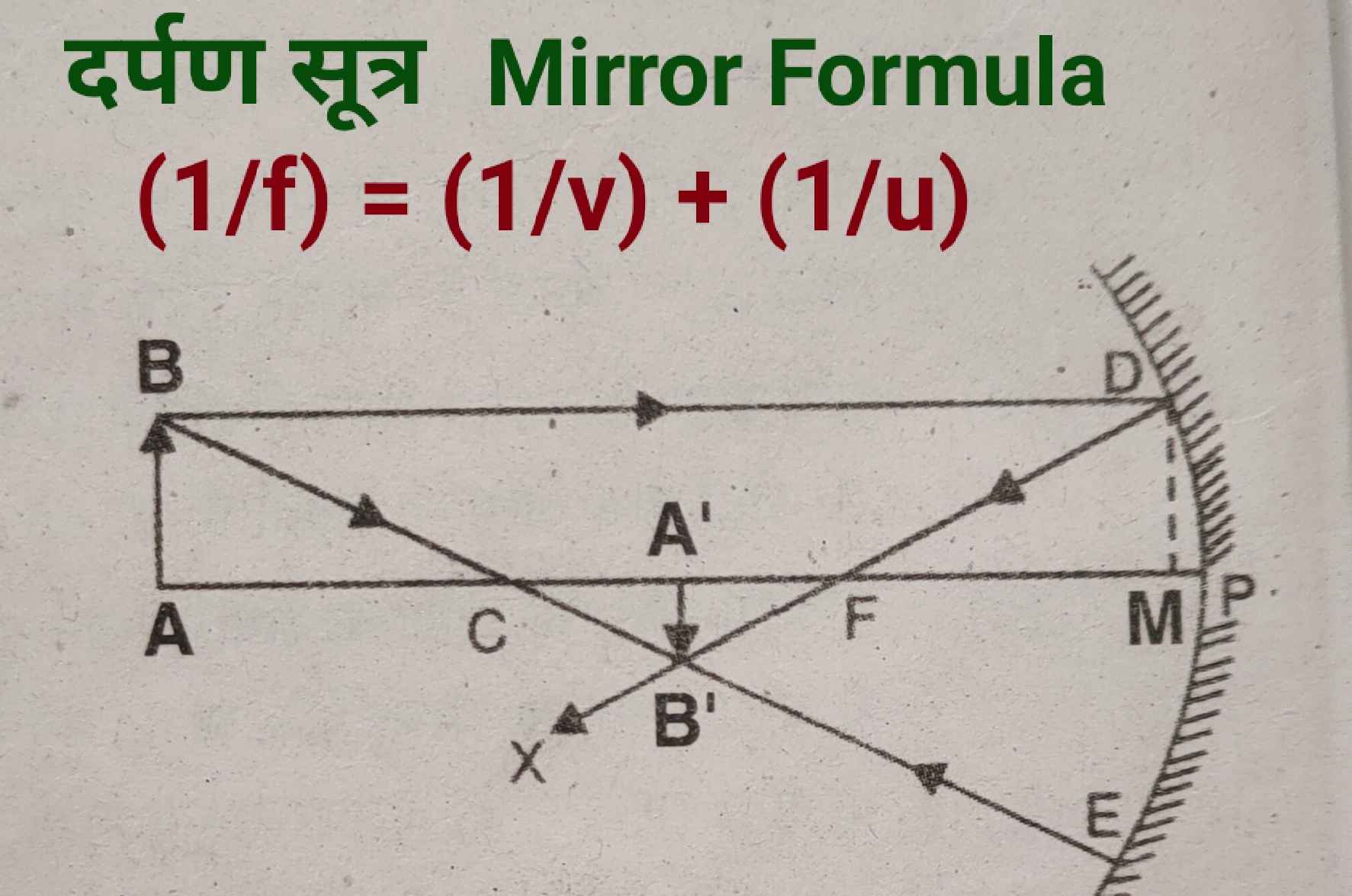
व्युत्पत्ति– मानलो एक अवतल दर्पण DPE है। इस अवतल दर्पण के सामने अनन्त और वक्रता केन्द्र के मध्य एक वस्तु रखी है। इस वस्तु का प्रतिबिम्ब मुख्य फोकस और वक्रता केन्द्र के मध्य बनता है। बिन्दु D से मुख्य अक्ष पर अभिलम्ब DM डाला गया है।
अवतल दर्पण में,
ध्रुव = P
फोकस = F
वक्रता केन्द्र = C
वस्तु = AB
वस्तु का प्रतिबिम्ब = A'B'

Derivation– Let be a concave mirror DPE. An object is placed between infinity and center of curvature in front of this concave mirror. The image of this object is formed between the principal focus and the center of curvature. The normal DM is drawn from the point D to the principal axis.
In a concave mirror,
Pole = P
Focus = F
Center of curvature = C
Object = AB
Image of object = A'B'

भौतिक विज्ञान के इन 👇 प्रकरणों को भी पढ़ें। (Also read these 👇 episodes of Physics.)
गोलीय दर्पण की फोकस दूरी और वक्रता त्रिज्या में सम्बन्ध | f = R/2 || Focus Length = Radius Of Curvature/2

अवतल दर्पण में चिह्न परिपाटी के अनुसार–
दर्पण के ध्रुव से वस्तु की दूरी PA = -u
दर्पण के ध्रुव से प्रतिबिम्ब की दूरी PA' = -v
वस्तु की फोकस दूरी PF = -f
दर्पण की वक्रता त्रिज्या PC = -R

According to the convention of marking in a concave mirror–
Distance of the object from the pole of the mirror PA = -u
Distance of the image from the pole of the mirror PA' = -v
Focus distance of the object PF = -f
Radius of curvature of mirror PC = -R

भौतिक विज्ञान के इन 👇 प्रकरणों को भी पढ़ें। (Also read these 👇 episodes of Physics.)
उत्तल दर्पण में प्रतिबिम्ब किस प्रकार बनते हैं? | How Are Images Formed In A Convex Mirror?

चित्र से स्पष्ट है कि त्रिभुज ABC तथा त्रिभुज A'CB' समरूप हैं। समरूप त्रिभुजों की सम्मुख भुजाओं के अनुपात समान होते हैं।
अतः (AB⁄A'B') = (CA⁄A'C) ...............1
इसी प्रकार त्रिभुज FA'B' और त्रिभुज FMD भी समरूप हैं।
अतः (MD⁄A'B') = (MF⁄FA')
यदि अवतल दर्पण का द्वारक छोटा हो, तो MD = AB
इसलिए (AB⁄A'B') = (MF⁄FA') .............2
समीकरण 1 और समीकरण 2 से,
(CA⁄A'C) = (MF⁄FA')
यदि बिन्दु M, ध्रुव P के निकट स्थित हो, तो MF = PF
इसलिए (CA⁄A'C) = (PF⁄FA')

From the figure it is clear that triangle ABC and triangle A'CB' are similar. The opposite sides of similar triangles have the same ratio.
Therefore (AB⁄A'B') = (CA⁄A'C) ...............1
Similarly triangle FA'B' and triangle FMD are also similar.
Therefore (MD⁄A'B') = (MF⁄FA')
If the aperture of a concave mirror is small, then MD = AB
Therefore (AB⁄A'B') = (MF⁄FA') .............2
From Equation 1 and Equation 2,
(CA⁄A'C) = (MF⁄FA')
If point M lies near pole P, then MF = PF
Therefore (CA⁄A'C) = (PF⁄FA')

भौतिक विज्ञान के इन 👇 प्रकरणों को भी पढ़ें। (Also read these 👇 episodes of Physics.)
अवतल दर्पण में प्रतिबिम्ब किस प्रकार बनते हैं? | How Are Images Formed In Concave Mirror?

(CA⁄A'C) = (PF⁄FA')
चित्र के अनुसार,
[(PA-PC)⁄(PC-PA')] = [(PF)⁄(PA'-PF)]
{(-u)-(-R)}⁄{(-R)-(-v)} = (-f)⁄{(-v)-(-f)}
(u-R)⁄(R-v) = (f)⁄(v-f)
(u-R)(v-f) = (f)(R-v)
uv-uf-vR+fR = fR-vf
uv = uf+vR-vf
हम जानते हैं कि R = 2f
अतः uv = uf+(v×2f)-vf
uv = uf+2vf-vf
uv = uf+vf
दोनों पक्षों में uvf का भाग देने पर,
(1⁄f) = (1⁄v) + (1⁄u)
या (u+v)⁄uv = 1⁄f
अतः f = uv⁄(u+v)
यही सिद्ध करना था।

(CA⁄A'C) = (PF⁄FA')
As per the picture,
[(PA-PC)⁄(PC-PA')] = [(PF)⁄(PA'-PF)]
{(-u)-(-R)}⁄{(-R)-(-v)} = (-f)⁄{(-v)-(-f)}
(u-R)⁄(R-v) = (f)⁄(v-f)
(u-R)(v-f) = (f)(R-v)
uv-uf-vR+fR = fR-vf
uv = uf+vR-vf
We know that R = 2f
Therefore uv = uf+(v×2f)-vf
uv = uf+2vf-vf
uv = uf+vf
On dividing the uvf on both the sides,
(1⁄f) = (1⁄v) + (1⁄u)
Or (u+v)⁄uv = 1⁄f
Therefore f = uv⁄(u+v)
This was to prove it.

भौतिक विज्ञान के इन 👇 प्रकरणों को भी पढ़ें। (Also read these 👇 episodes of Physics.)
गोलीय दर्पण क्या है? | अवतल और उत्तल दर्पण || What Is Spherical Mirror? | Concave And Convex Mirror

दर्पण सूत्र में u, v तथा f का मान लिखते समय चिह्न परिपाटी के अनुसार ही चिह्नों का प्रयोग किया जाता है। अवतल दर्पण के लिए u और f के मान हमेशा ऋणात्मक होते हैं। वास्तविक प्रतिबिम्ब के लिए v का मान ऋणात्मक होता है। आभासी प्रतिबिम्ब के लिए v का मान धनात्मक होता है।

While writing the values ​​of u, v and f in the mirror formula, the symbols are used as per the mark convention. The values ​​of u and f are always negative for a concave mirror. For a real image, the value of v is negative. The value of v is positive for a virtual image.

भौतिक विज्ञान के इन 👇 प्रकरणों को भी पढ़ें। (Also read these 👇 episodes of Physics.)
दर्पण किसे कहते हैं? | समतल दर्पण में प्रतिबिम्ब कैसे बनता है? || Information About Plane Mirror

I hope the above information will be useful and important.
(आशा है, उपरोक्त जानकारी उपयोगी एवं महत्वपूर्ण होगी।)
Thank you.
R F Temre
pragyaab.com