
गोलीय दर्पण के लिए 'आवर्धन' | 'Magnification' For Spherical Mirror
आवर्धन (Magnification)
गोलीय दर्पण के सामने रखी वस्तु की स्थिति को परिवर्तित करने पर उसके प्रतिबिम्ब के आकार में भी परिवर्तन हो जाता है। गोलीय दर्पण में वस्तु की लम्बाई और प्रतिबिम्ब की लम्बाई मुख्य अक्ष के लम्बवत नापी जाती है। प्रतिबिम्ब की लम्बाई और वस्तु की लम्बाई के अनुपात को 'रेखीय आवर्धन' कहा जाता है। आवर्धन एक आपेक्षिक राशि है। इसके द्वारा प्रतिबिम्ब की लम्बाई और वस्तु की लम्बाई की तुलना की जाती है।
On changing the position of an object placed in front of a spherical mirror, the size of its image also changes. In a spherical mirror, the length of the object and the length of the image are measured perpendicular to the principal axis. The ratio of the length of the image to the length of the object is called 'linear magnification'. Magnification is a relative quantity. It compares the length of the image and the length of the object.
भौतिक विज्ञान के इन 👇 प्रकरणों को भी पढ़ें। (Also read these 👇 episodes of Physics.)
(1/f) = (1/v) + (1/u) दर्पण सूत्र की व्युत्पत्ति कीजिए | Derive The Mirror Formula
आवर्धन का गणितीय निरूपण (Mathematical Representation Of Magnification)
यदि किसी गोलीय दर्पण में प्रतिबिम्ब की लम्बाई 'I' और वस्तु की लम्बाई 'O'और आवर्धन 'm' हो, तो
आवर्धन (m) = प्रतिबिम्ब की लम्बाई⁄वस्तु की लम्बाई = A'B'⁄AB = I⁄O
If the length of the image in a spherical mirror is 'I' and the length of the object is 'O' and the magnification is 'm', then
Magnification (m) = length of the image⁄length of the object = A'B'⁄AB = I⁄O
भौतिक विज्ञान के इन 👇 प्रकरणों को भी पढ़ें। (Also read these 👇 episodes of Physics.)
गोलीय दर्पण के लिए चिह्न परिपाटी एवं इसके नियम | Mark Convention And Its Rules
आवर्धन के लिए चिह्न परिपाटी (Mark Convention For Magnification)
चिह्न परिपाटी के अनुसार, वस्तु की लम्बाई (AB) धनात्मक रहती है। यदि प्रतिबिम्ब वास्तविक और उल्टा बने, तो चिह्न परिपाटी के अनुसार प्रतिबिम्ब की लम्बाई को ऋणात्मक लिया जाता है। इस प्रकरण में आवर्धन का मान ऋणात्मक होगा। यदि प्रतिबिम्ब सीधा और आभासी बने, तो चिह्न परिपाटी के अनुसार प्रतिबिम्ब की लम्बाई को धनात्मक लिया जाएगा। ऐसी स्थिति में आवर्धन धनात्मक होगा।
As per the symbol convention, the length (AB) of the object remains positive. If the image is real and inverted, the length of the image is taken as negative as per the sign convention. In this case the value of magnification will be negative. If the image becomes erect and virtual, then the length of the image will be taken as positive as per the sign convention. In this case magnification will be positive.
भौतिक विज्ञान के इन 👇 प्रकरणों को भी पढ़ें। (Also read these 👇 episodes of Physics.)
गोलीय दर्पण की फोकस दूरी और वक्रता त्रिज्या में सम्बन्ध | f = R/2 || Focus Length = Radius Of Curvature/2
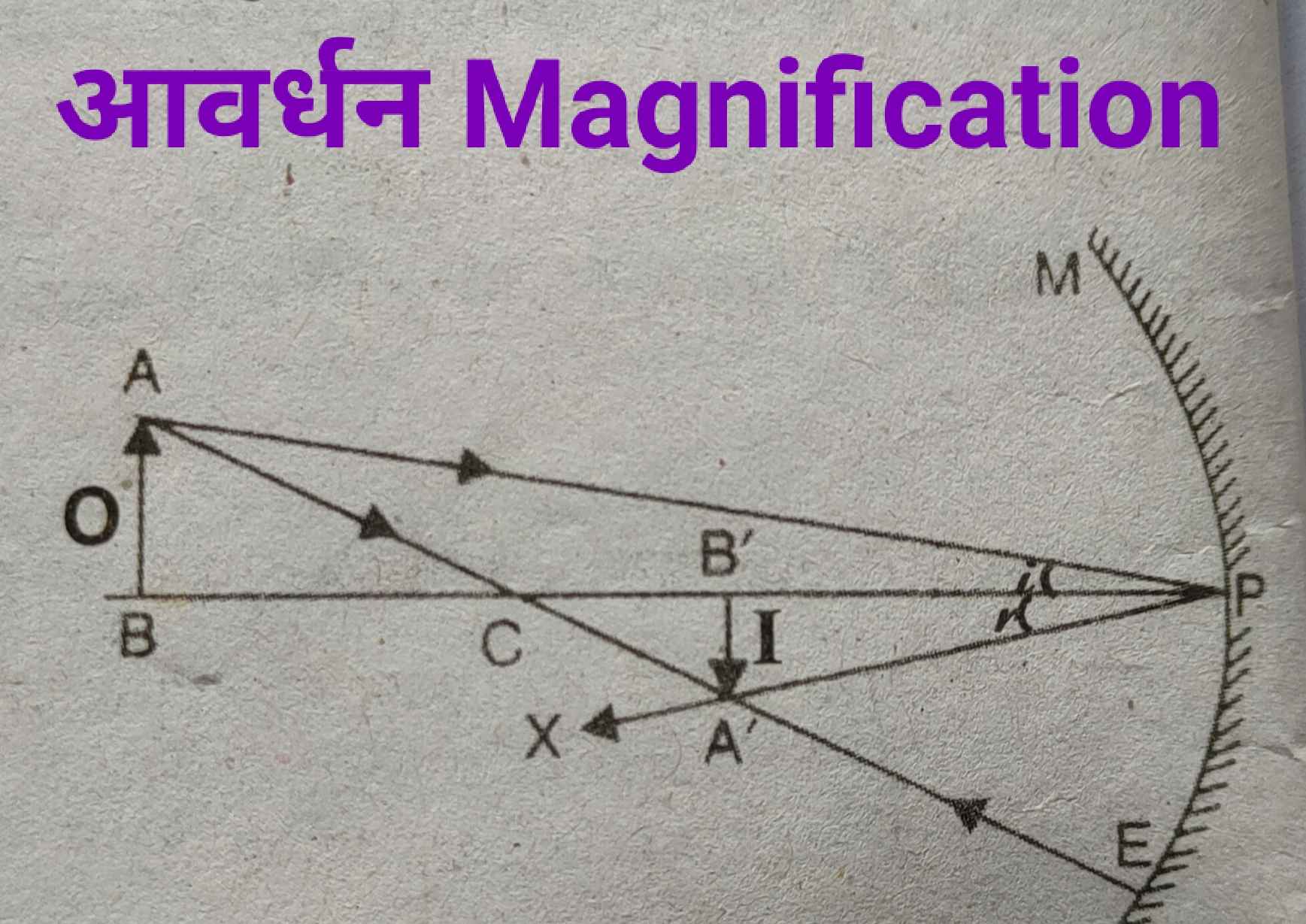
मानलो एक अवतल दर्पण MPE है। इस अवतल दर्पण में ध्रुव से वस्तु की दूरी u तथा ध्रुव से प्रतिबिम्ब की दूरी v है। प्रतिबिम्ब वास्तविक और उल्टा बनता है। अतः चिन्ह परिपाटी के अनुसार,
आवर्धन m = (-I)⁄O = [-(-v)]⁄(-u) = (-v)⁄u
Assume a concave mirror MPE. In this concave mirror the distance of the object from the pole is u and the distance of the image from the pole is v. The image becomes real and inverted. So as per the sign convention,
Magnification m = (-I)⁄O = [-(-v)]⁄(-u) = (-v)⁄u
भौतिक विज्ञान के इन 👇 प्रकरणों को भी पढ़ें। (Also read these 👇 episodes of Physics.)
उत्तल दर्पण में प्रतिबिम्ब किस प्रकार बनते हैं? | How Are Images Formed In A Convex Mirror?
आशा है, उपरोक्त जानकारी उपयोगी एवं महत्वपूर्ण होगी।
(I hope the above information will be useful and important. )
Thank you.
R. F. Tembhre
(Teacher)
pragyaab.com




Comments